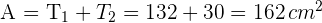Kapitel
- Definition von Umfang und Flächeninhalt
- Umfang und Flächeninhalt von Dreiecken
- Umfang und Fläche eines Quadrats
- Umfang und Fläche eines Rechtecks
- Umfang und Fläche einer Raute
- Umfang und Fläche eines Parallelogramms
- Umfang und Fläche eines Trapez
- Umfang und Fläche eines regelmäßigen Vielecks
- Umfang und Fläche eines unregelmäßigen Vielecks
Definition von Umfang und Flächeninhalt
Der Umfang eines Vielecks ist gleich der Summe der Längen seiner Seiten.
Der Flächeninhalt eines Vielecks ist das Maß für die vom Vieleck umschlossene Region oder Fläche.
Umfang und Flächeninhalt von Dreiecken
Der Umfang eines Dreiecks ergibt sich aus der Addition der Längen seiner drei Seiten. Je nach Art des Dreiecks hast du die folgenden Formeln für den Umfang
| Gleichseitiges Dreieck | Gleichschenkliges Dreieck | Unregelmäßiges Dreieck |
 |  |  |
 |  |  |
Der Flächeninhalt eines Dreiecks ist gleich der Hälfte des Produkts aus seiner Grundseite und seiner Höhe.
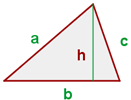
Für das Dreieck mit der Grundseite 
und der Höhe 
lautet die Formel für den Flächeninhalt
Beispiel: Finde die Fläche und den Umfang des folgenden Dreiecks
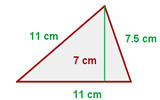
Es handelt sich um ein gleichschenkliges Dreieck, also ist der Umfang
Du bemerkst, dass die Grundseite 
und die Höhe 
ist
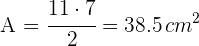
Umfang und Fläche eines Quadrats
Der Umfang eines Quadrats ergibt sich aus der Addition der Längen seiner vier Seiten; da alle vier Seiten gleich sind, lautet die Formel für den Umfang eines Quadrats der Seite 
Um den Flächeninhalt eines Quadrats herauszufinden, quadrierst du die Seiten des Quadrats.
Beispiel: Berechne die Fläche und den Umfang des Quadrats der Seite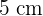 
.
Die Seite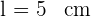 
. Du berechnest den Umfang
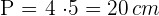
Du berechnest die Fläche
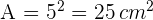
Umfang und Fläche eines Rechtecks
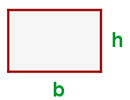
Der Umfang eines Rechtecks ergibt sich aus der Addition der Längen seiner vier Seiten; die Formel für den Umfang eines Rechtecks mit der Grundseite und der Höhe lautet
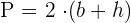
Um den Flächeninhalt eines Rechtecks zu ermitteln, multiplizierst du seine Grundseite mit seiner Höhe
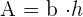
Beispiel: Berechne die Fläche und den Umfang des Rechtecks mit 
Grundseite und 
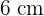Höhe.
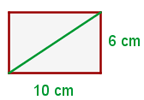
Berechne den Umfang
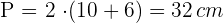
Berechne die Fläche
Umfang und Fläche einer Raute
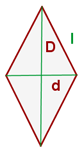
Den Umfang einer Raute erhält man durch Addition der Längen ihrer vier Seiten; da diese gleich sind, lautet die Formel für den Umfang einer Raute der Seite
Um den Flächeninhalt einer Raute mit der Hauptdiagonale 
und der Nebendiagonale 
zu ermitteln, wendest du die Formel an, um die Hälfte des Produkts der Diagonalen zu berechnen
Beispiel: Berechne den Flächeninhalt und den Umfang der Raute, deren Diagonalen 
und 
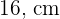messen und deren Seite 
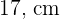misst.
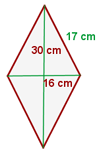
Berechne den Umfang
Berechne die Fläche
Umfang und Fläche eines Parallelogramms
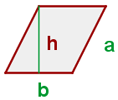
Den Umfang eines Parallelogramms erhältst du durch Addition der Längen seiner vier Seiten; da die gegenüberliegenden Seiten gleich sind, lautet die Formel für den Umfang eines Parallelogramms mit den Seiten 
und
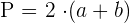
Um den Flächeninhalt eines Parallelogramms mit der Grundfläche und der Höhe zu ermitteln, wendest du die Formel an, die sich aus dem Produkt von Grundseite und Höhe ergibt.
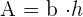
Beispiel: Berechne den Flächeninhalt und den Umfang des Parallelogramms, dessen Seiten 
und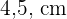 
messen und dessen Höhe 
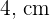beträgt.
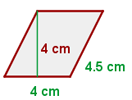
Berechne den Umfang
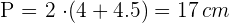
Berechne die Fläche
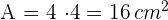
Umfang und Fläche eines Trapez
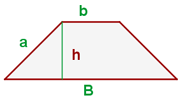
Der Umfang eines Trapezes ergibt sich aus der Addition der Längen seiner vier Seiten, d. h.
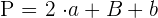
Um den Flächeninhalt eines Trapezes mit der Grundseite 
, der gegenüberliegenden Seite und der Höhe zu ermitteln, gilt die Formel, die sich aus dem halben Produkt der Höhe und der Summe der beiden Flächen ergibt
Beispiel: Berechne den Flächeninhalt und den Umfang des Trapezes, dessen große und kleine Seite 
bzw. 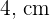messen, dessen schräge Seiten 
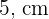und dessen Höhe 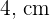misst.
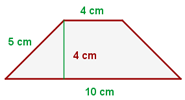
Berechne den Umfang
Berechne die Fläche
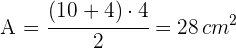
Umfang und Fläche eines regelmäßigen Vielecks
Der Umfang eines regelmäßigen Vielecks von 
Seiten Länge ist
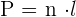
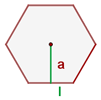
Um den Flächeninhalt eines regelmäßigen Vielecks mit der Seite und dem Apothema zu ermitteln, gilt die Formel, die sich aus dem halben Produkt von Umfang und Apothema ergibt
Beispiel: Berechne die Fläche und den Umfang eines regelmäßigen Fünfecks mit der Seite 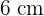, dessen Abstand vom Mittelpunkt zu einem seiner Eckpunkte 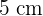beträgt.
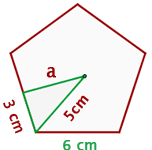
Berechne den Umfang
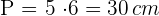
Berechne den Flächeninhalt. Wende dazu den Satz des Pythagoras an und erhalte den Wert des Apothemas
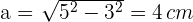
Setze den Umfang und das Apothema in die Formel für die Fläche ein
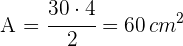
Beispiel: Berechne das Apothema und den Umfang eines regelmäßigen Sechsecks, das in einen Kreis mit dem Radius 
eingeschrieben ist.
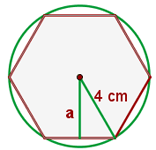
Da es sich um ein Sechseck handelt, kannst du es in sechs gleiche gleichseitige Dreiecke unterteilen, wobei du erhältst, dass jede Seite misst. Du berechnest den Umfang
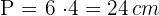
Berechne das Apothema. Verwende hierzu den Satz des Pythagoras und erhalte
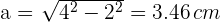
Umfang und Fläche eines unregelmäßigen Vielecks
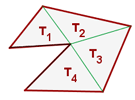
Den Umfang eines unregelmäßigen Vielecks erhältst du, indem du alle Seiten zusammenzählst
Unterteile, um den Flächeninhalt eines unregelmäßigen Vielecks zu ermitteln, das Vieleck in Dreiecke und addierst die Flächeninhalte der einzelnen Dreiecke.
Beispiel: Berechne die Fläche und den Umfang des folgenden Vielecks
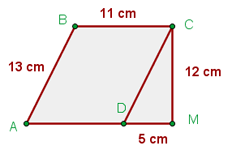
Berechne den Umfang
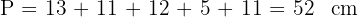
Berechne den Flächeninhalt. Berechne dazu den Flächeninhalt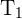 
des Parallelogramms 
und den Flächeninhalt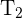 
des Dreiecks 
.
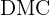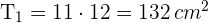
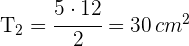
Der Flächeninhalt des unregelmäßigen Vielecks ist also
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
